The Mathematical Prediction of the Earth's Pole Motion

L.D. Akulenko, S.A. Kumakshev, and A.M. Shmatkov

Russian Academy of Sciences

Institute for Problems in Mechanics named after A.Ju. Ishlinsky

Let us try to understand without formulas what causes the motion of the pole. If you are familiar with theoretical mechanics, you may skip to the prediction.

Imagine the Earth to be a ball rotating about the vertical axis. If an asteroid hits such a ball so that the impact occurs tangentially to the equator, almost nothing will happen which could be of interest from the "cosmic" point of view. Only the speed of the rotation will increase (or decrease). Even if the impact occurs in the middle latitude region, where we live, rather than on the equator, the axis of rotation will only slightly change its direction. However, if we take into account that the Earth is flattened by 21400 meters along the vertical, we will obtain an interesting result. It turns out that the axis of rotation will perform circular motions. In science, such motions are called the precession motions. A great scientist Leonhard Euler in the middle of the XVIII-th century calculated that the axis of rotation performs a full circle in 305 days. To common surprise, an astronomer Chandler, observing the motion of stars, discovered in 1891 that in fact a full circle requires about 433 days.

The point is that the Earth consists not of a rigid material but of a substance that resembles rubber. Everyone has heard about oceanic tides, but only few people know that the gravitational forces cause similar tides also in the Earth's crust. In such tides, the formations that we usually regard as rigid stones extend, elevating and lowering by about a meter. Had the Moon and the Sun disappeared, this tidal wave would have been running around The Earth for a very long time, if the "rubber" were good. In fact, however, this wave would have decayed in several hours and its energy would transform into heat. But the Sun and the Moon do not have the habit to hide and maintain the attraction of both the ocean and rocks. As a result, the tides heat the Earth and gradually slow down its rotation, the period of the rotation increasing approximately by 17 ten-thousandths of second per hundred years.

The same fate should have befallen the precession motion even substantially quicker. Even if the Earth had been once hit by an asteroid at a time immemorial, the oscillations of the Earth's axis caused by the impact would have completely decayed in a couple of hundred years. Observations, however, show that the oscillations do not decay. The axis of rotation of the Earth permanently changes its direction. What is the force that makes North and South Poles move permanently? The attraction of the Sun and the Moon!

This point needs an elucidation. If the Sun had moved relative to the Earth in the equatorial plane, then the parts of our planet, both south and the north of the equator, would have always been attracted identically. But the plane in which the Sun moves is inclined by approximately 66 degrees. Therefore, these parts are attracted differently during the year. It results as if the Sun slightly rocks the Earth and, since the Earth is not exactly a ball, the precession motion arises.

If we look at the phenomenon more attentively, even more interesting picture will appear. We have fully forgotten about the Moon! The influence of the Earth and the Moon on the Sun is negligible, whereas the influence of the motion of the Moon on that of the Earth is highly significant. If we investigate this influence thoroughly, we will see that the Sun and the Moon push the Earth in such a way that the precession oscillations increase. In science, this phenomenon is called the resonance. As a result, the poles of the Earth move several meters a year. If we do not want an automobile navigator to lead us to the oncoming traffic lane, it is necessary to be able not only to measure this motion but also to predict it.

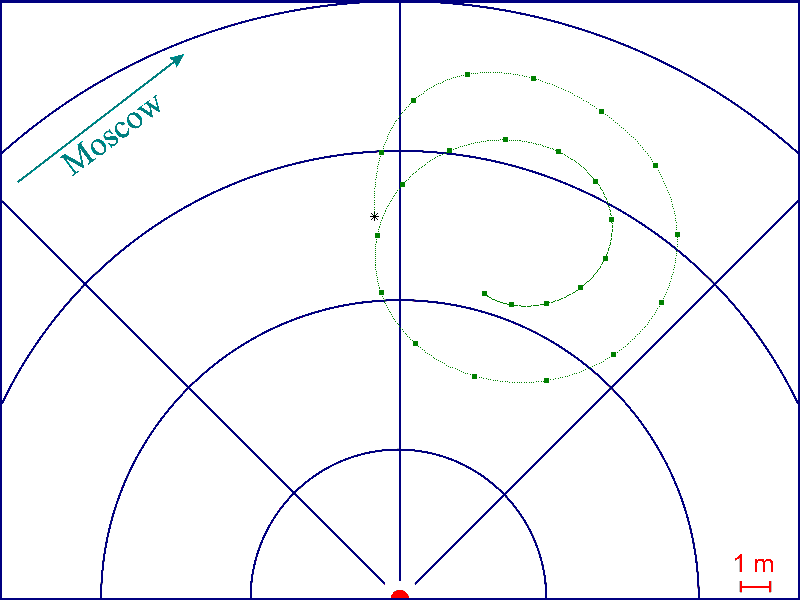
In the figure below, green points show the prediction of the motion of the North Pole for 750 days ahead. Each 30 days are marked by a square. A red circle marks the "standard" North Pole used for determining the geographic coordinates. The exact current position of the Earth's axis of rotation is shown by an asterisk. The information below the figure is addressed to experts and can be skipped.

Information for the experts

The prediction file consists of the three columns with the data for 900 days. The first gives the date in the MJD format, while the second and the third contain the pole coordinates X and Y in arc seconds. Abscissa is directed towards Greenwich. We'll do our best to update the prediction every week.

Download the prediction of the Earth Pole motion for 900 days

The following file contains the threoretical bases of the prediction.

Download file

Acknowledgements

The authors thanks N.N. Bolotnik, A.V. Manzhirov, and A.D. Polyanin for their assistance.

This Web page is supported by the program "Leading Scientific Schools" (project no. 4315.2008.1) and Russian Foundation for Basic Research (project nos. 08-01-00411 and 08-08-00292).

References

Books

E.W. Woolard Theory of the rotation of the Earth around its center of mass. Astron. 1953. Pap. Amer. Eph. Naut. Almanac XV, 1, 1-165.
W.H. Munk and G.J.F. Macdonald The Rotation of the Earth. Cambridge University Press, 1960.
P. Melchior Physique et Dynamique Planetaires, Geodynamique. Vander, Vol. 4, 1972.
H. Moritz and I.I. Muller Earth Rotation: Theory and Observation, Ungar, New York, 1987.
Yu.N. Avsjuk Tidal Forces and Natural Processes. Moscow: UIPE RAS, 1996. 188 pp.
N.S. Sidorenkov Physics of the Eart's Rotation Instabilities. Moscow: Nauka, Publishing Company Fizmatlit, 2002, 384 pp.
C. Audoin and B. Guinot The Measurement of Time: Time, Frequency, and the Atomic Clock. Cambridge University Press, 2001. 346 pp.

Papers

Int. Earth Rotation Service (IERS) Annual Reports. Central Burea of IERS. Observatoire de Paris. Verlag BKG: Frankfurt am Mein.
JOURNÉES. Observatoire de Paris.
S. Chandler On the variation in latitude // Astron. J., 1891. V. 11. P. 83.
J. Vondrak Earth Rotation Parameters 1899.7—1992.0 after Reanalysis within the Hipporcos Frame // Surveys Geophys. 1999. 20. P. 169-195.
B. Guinot The Chandlerian nutation from 1900 to 1980 // Geophys. J. Roy. Soc. 1982. V. 71. P. 295-301.
N. Capitane, B. Guinot, and D.D. McCarthy Definition of the Celestial Ephemeries origin and UT1 in the International Reference Frame // Astron. Astrophys. 2000. 355. P. 398-405.
L.D. Akulenko, Yu.G. Markov, and L.V. Rykhlova Motion of the Earth's Poles under the Action of Gravitational Tides in the Deformable-Earth Model// Doklady Physics. 2001. V. 46. N 4. Pp. 261-263.
L.D. Akulenko, S.A. Kumakshev, and Yu.G. Markov Modeling of the Pole's Motion for a Deformable Earth// Doklady Physics. 2001. V. 46, N 7. Pp. 508-512.
L.D. Akulenko, S.A. Kumakshev, and Yu.G. Markov Motion of the Earth's Pole// Doklady Physics. 2002. V. 47, N 1. Pp. 78-84.
L.D. Akulenko, S.A. Kumakshev, and Yu.G. Markov Model of the Gravitational-Tidal Mechanism of Exciting Oscillations of the Earth's Pole// Doklady Physics. 2005. V. 50, N 2. Pp. 106-111.
L.D. Akulenko, S.A. Kumakshev, Yu.G. Markov, and L.V. Rykhlova A Model for the Polar Motion of the Deformable Earth Adequate for Astrometric Data// Astronomy Reports. 2002. V. 46. N 1. Pp. 74-82.
L.D. Akulenko, S.A. Kumakshev, Yu.G. Markov, and L. V. Rykhlova Forecasting the Polar Motions of the Deformable Earth// Astronomy Reports. 2002. V. 46. N 10. Pp. 858-866.
L.D. Akulenko, S.A. Kumakshev, Yu.G. Markov, and L. V. Rykhlova A Gravitational-Tidal Mechanism for the Earth's Polar Oscillations// Astronomy Reports. 2005. V. 49. N 10. Pp. 847-857.
L.D. Akulenko, S.A. Kumakshev, Yu.G. Markov, and L.V. Rykhlova High-Accuracy Forecasting of the Earth's Polar Motion// Astronomy Reports. 2006. V. 50. N 4. Pp. 333-341.
L.D. Akulenko, S.A. Kumakshev, Yu.G. Markov, and L.V. Rykhlova Analysis of Multifrequency Effects in Oscillations of the Earth's Pole// Astronomy Reports. 2007. V. 51. N 5. Pp. 421-427.
L.D. Akulenko, S.A. Kumakshev, and Yu.G. Markov A Celestial Mechanics Model of Oscillations of the Poles of a Deformable Earth// Cosmic Research. 2005. V. 43. N 5. Pp. 335-341.
L.D. Akulenko, S.A. Kumakshev, and Yu.G. Markov Perturbed Earth rotation// Mechanics of Solids. 2005. V. 40. N 5. Pp. 12-19.