Лаборатория механики сложных жидкостей. Подробная информация
См. также Общие сведения о лаборатории
См. также Юбилейные материалы и достижения 2015–2025 к 60-летию ИПМех РАН
См. также Наши результаты: Удар импульсной микроструи по микроволокну
См. также Наши результаты: Деформация и фрагментация капли при столкновении с тонким цилиндром
Основные достижения
- Установлен эффект подавления процесса разрушения и регуляризации стоячей гравитационной волны при помощи слоя плавающих частиц (Калиниченко В.А., 2019).
- Импульсное радиальное истечение жидкости из зазора между двумя быстро сближающимися дисками использовано как метод для реологических испытаний упругих жидкостей в режиме экстремальных деформаций (высокие скорости деформации и степени растяжения). Построено теоретическое описание радиального истечения упругой жидкости в рамках реологической модели Олдройд-Б (Oldroyd-B). Проведены тестовые эксперименты по метанию водных растворов высокомолекулярного полиэтиленоксида (ПЭО) концентраций 1, 2, 4%. Путем сопоставления теоретических предсказаний с экспериментальными данными определены реологические характеристики испытанных растворов ПЭО в экстремальных деформационных условиях. Наблюдается значительное увеличение модуля упругости и уменьшение времени релаксации при высоких скоростях деформаций. Метод применим для реологических испытаний полимерных и биологических жидкостей в медицине, биологии и в ряде химических технологий (Базилевский А.В. и Рожков А.Н., 2018).

Жидкость импульсно истекает радиально со скоростью ~1-10 м/с из кольцевого зазора между двумя сближающимися дисками; начальная толщина зазора ~2 мм, время истечения ~1 мс: а-е – вода, глицерин, растворы полиэтиленоксида концентраций 0.1, 1, 2 и 4%. Положение зазора отмечено стрелкой.
- Выполнено численное моделирование гравитационной концентрационной конвекции воды с растворенной примесью в прямоугольном геотермальном резервуаре, на верхней границе которого поддерживается постоянная концентрация примеси. Получено, что около верхней границы хаотически возникают мелкомасштабные солевые «пальцы», которые при опускании сливаются и укрупняются; со временем рождающиеся мелкомасштабные «пальцы» объединяются в группы. Исследовано влияние пористости на время развития конвекции и характеристики массопереноса в однородной геотермальной системе (Соболева Е.Б. и Цыпкин Г.Г., 2016).
- Исследовалась деформация водонасыщенной области при фильтрации в пористой среде с изменяющимся капиллярным давлением. Показано, что в случае неустойчивости течения градиент капиллярного давления, направленный вдоль поверхности раздела между жидкостью и газом, приводит к деформации области, которая со временем делится на две не связанные области. Предполагается, что рассматриваемый процесс описывает один из возможных механизмов фрагментация фильтрационных течений, которые могут приводить к образованию остаточной нефти при эксплуатации нефтяных месторождений и засолению грунтов при испарении грунтовых вод, содержащих растворенную примесь (Tsypkin G.G. and Shargatov V.A., 2018).
- Выполнено численное моделирование роста температуры сверхкритической жидкости за счет поршневого эффекта (нагрева при адиабатическом сжатии, происходящего из-за высокой сжимаемости среды). Получено, что вблизи критической точки при характерное время поршневого эффекта перестает уменьшаться и стремится к постоянной величине, отклоняясь от теоретически предсказанной зависимости, что указывает на нелинейный характер явления. При достаточно больших температурах нагрев переходит в режим теплопроводности. Здесь ε=(T–Tc)/Tc – температурное «расстояние» до критической точки; T, Tc –текущее и критическое значения температуры (Gorbunov A. and Soboleva E., 2020).
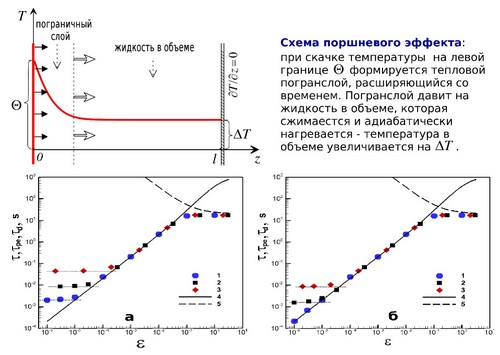
Время поршневого эффекта τ при скачке температуры Θ=0.1 (1), 1 (2), 10 мК (3) в области шириной 1 см в зависимости от ε. Среда описывается кубическим уравнением Ван-дер-Ваальса (а) или уравнением состояния пятой степени (б). Теоретическая кривая поршневого эффекта τpe(ε) (4), кривая теплопроводности τd(ε) (5).
- Результаты математического моделирования нестационарных режимов генерации внутренних и поверхностных гравитационных показывают, что волновые поля от нестационарных источников возмущений при определенных режимах генерации представляют собой гибридную систему волн двух типов: кольцевых (поперечных) и клиновидных (продольных). Нестационарность источника возмущений приводит к появлению не только кольцевых волн, расходящихся по непосредственно от источника, но также к генерации гибридных волновых возмущений, распространяющихся от источника вверх по потоку. Качественная картина волновых полей от нестационарного источника существенно усложняется по сравнению со случаем генерации волн движущимся стационарным источником, когда в фиксированную точку наблюдения последовательно приходят волновые фронты отдельных клиновидных (продольных) мод. При определенных параметрах генерации в фиксированную точку наблюдения могут приходить вначале кольцевые (поперечные) волны. Волновые моды, первые достигающей фиксированной точки наблюдения, определяются параметрами генерации и стратификацией среды. Для больших номеров мод угол полураствора волнового клина Кельвина уменьшается с номером моды так же, как и для случаев стационарных режимов генерации. Полученные результаты математического моделирования полей внутренних и поверхностных гравитационных волн дают возможность эффективно анализировать основные амплитудно-фазовые характеристики возбуждаемых волновых полей, и, кроме того, качественно исследовать полученные решения, что важно для правильной постановки более сложных математических моделей волновой динамики реальных стратифицированных сред. Подобного рода волновые картины могут наблюдаться при дистанционном зондировании, наблюдении и измерениях внутренних и поверхностных гравитационных волн, возбуждаемых различными источниками возмущений, в природных (океан, атмосфера Земли) и искусственных стратифицированных средах (Булатов В.В. и Владимиров Ю.В., 2018).
История
Базой для создания Лаборатории механики сложных жидкостей послужили Лаборатория прикладной механики сплошных сред, которой до 1994 года руководил профессор Владимир Маркович Ентов, и Лаборатория математического и физического моделирования в гидродинамике, руководимая до 2010 года профессором Вадимом Ивановичем Полежаевым. В настоящее время лабораторией руководит доктор физико-математических наук Алексей Николаевич Рожков.
Общая информация
Лаборатория механики сложных жидкостей продолжает и развивает исследования, заложенные в лабораториях Института проблем механики, которыми в своё время руководили профессора Лев Алексеевич Чудов, Вадим Брониславович Либрович, Владимир Маркович Ентов и Вадим Иванович Полежаев.
Сегодня в составе лаборатории 7 докторов и 5 кандидатов наук. В разное время сотрудники лаборатории были удостоены научных наград: Премия РАН им. К.Э. Циолковского (В.И. Полежаев, С.А. Никитин, 2003); Премия им. Г.И. Петрова (В.И. Полежаев, О.А. Бессонов, А.А. Горбунов, С.А. Никитин, Е.Б. Соболева, 2006); Премии им. Г.В. Виноградова Реологического общества (А.В. Базилевский и А.Н. Рожков, 2017); Премия и медаль им. Л.И. Седова (Г.Г. Цыпкин, 2017); Tanasawa Award, Institute of Liquid Atomization and Spray Systems – International (A. Rozhkov, 2009).
Наиболее значимые публикации сотрудников лаборатории
Книги
- Bulatov V.V., Vladimirov Yu.V. A general approach to ocean wave dynamics research: modelling, asymptotics, measurements. М.: Издательство «ОнтоПринт», 2019. 587 с. ISBN 978-5-00121-132-7
- Цыпкин Г.Г. Течения с фазовыми переходами в пористых средах. М.: Наука. Физматлит. 2009. 230 с.
ISBN 978-5-9221-1102-7
Статьи
- Базилевский А.В., Калиниченко В.А., Рожков А.Н. Вязкая регуляризация разрушающихся волн Фарадея // Письма в ЖЭТФ. 2018. Т. 107. № 11-12. C. 717–722.
DOI: 10.7868/S0370274X1811005X
[math-net]
= Bazilevskii A.V., Kalinichenko V.A., Rozhkov A.N. Viscous Regularization of Breaking Faraday Waves. JETP Letters. 2018. V. 107. No. 11. P. 684-689.
DOI: 10.1134/S0021364018110061
- Базилевский А.В., Рожков А.Н. Всплеск упругой жидкости – реологический тест полимерных растворов // Высокомолекулярные соединения. Серия А. 2018. Т. 60. № 3. С. 235–248.
DOI: 10.7868/S2308112018030082
= Bazilevskii A.V., Rozhkov A.N. Splash of an elastic liquid as a rheological test of polymer solutions. Polymer Science. Series A. 2018. V. 60. No. 3. P. 391-403.
DOI: 10.1134/S0965545X1803001X
- Булатов В.В., Владимиров Ю.В. Аналитические решения уравнения внутренних гравитационных волн в полубесконечном слое стратифицированной среды переменной плавучести // Журнал вычислительной математики и математической физики. 2019. Т. 59. № 5. С. 792-795.
DOI: 10.1134/S0044466919050053
= Bulatov V.V., Vladimirov Y.V. Analytical solutions of the internal gravity wave equation for a semi-infinite stratified layer of variable buoyancy. Computational Mathematics and Mathematical Physics. 2019. V. 59. No. 5. P. 747-750.
DOI: 10.1134/S0965542519050051
- Булатов В.В. Владимиров Ю.В. Дальние поля внутренних гравитационных волн при нестационарных режимах генерации // Океанология. 2018. Т. 58. № 6. С. 875–881.
DOI: 10.1134/S0030157418060035
= Bulatov V.V., Vladimirov Y.V. Far fields of internal gravity waves from a nonstationary source. Oceanology. 2018. V. 58. No. 6. P. 796-801.
DOI: 10.1134/S0001437018060036
- Булатов В.В., Владимиров Ю.В. Внутренние волны, возбуждаемые источником в среде переменной плавучести // Известия РАН. Механика жидкости и газа. 2018. № 5. С. 38-44.
DOI: 10.31857/S056852810001778-6
= Bulatov V.V., Vladimirov Y.V. Internal waves excited by a moving source in a medium of variable buoyancy. Fluid Dynamics. 2018. V. 53. No. 5. P. 616-622.
DOI: 10.1134/S001546281805004X
- Калиниченко В.А. Регуляризация гравитационных баротропных волн в двухслойной жидкости // Изв. РАН. МЖГ. 2019. № 6. С. 1-13.
DOI: 10.1134/S0568528119060069
= Kalinichenko V.A. Regularization of barotropic gravity waves in a two-layer fluid. Fluid Dynamics. 2019. V. 54. No. 6. P. 761-773.
DOI: 10.1134/S0015462819060065
- Соболева Е.Б. Адиабатический нагрев (охлаждение) сверхкритической жидкости при изменении ее физических свойств // Изв. РАН. МЖГ. 2017. № 1. С. 28-39.
DOI: 10.7868/S0568528117010145
= Soboleva E.B. Adiabatic heating (cooling) of a supercritical fluid with variation in its physical properties. Fluid Dynamics. 2017. V. 52. No. 1. P. 25-36.
DOI: 10.1134/S0015462817010033
- Соболева Е.Б., Цыпкин Г.Г. Режимы концентрационной конвекции при испарении грунтовых вод, содержащих растворенную примесь // Изв. РАН. МЖГ. 2016. № 3. С. 70-78.
DOI: 10.7868/S0568528116030142
= Soboleva E.B., Tsypkin G.G. Regimes of haline convection during the evaporation of groundwater containing a dissolved admixture. Fluid Dynamics. 2016. V. 51. No. 3. P. 364-371.
DOI: 10.1134/S001546281603008X
- Федюшкин А.И. Влияние конвекции на кристаллизацию фосфата кальция в термостате в земных и космических условиях // Изв. РАН. МЖГ. 2020. № 4. С. 35-46.
DOI: 10.31857/S0568528120040040
= Fedyushkin A.I. Effect of convection on crystal growth of calcium phosphate in a thermostat under terrestrial and space conditions. Fluid Dynamics. 2020. V. 55. No. 4. P. 465-476.
DOI: 10.1134/S0015462820040047
- Цыпкин Г.Г. Термодинамические условия образования гидрата CO2 при инжекции углекислоты в пласт, содержащий гидрат метана // Изв. РАН. МЖГ. 2018. № 5. С. 103-112.
DOI: 10.31857/S056852810001798-8
= Tsypkin G.G. Thermodynamic conditions of formation of CO2 hydrate in carbon dioxide injection into a methane hydrate reservoir. Fluid Dynamics. 2018. V. 53. No. 5. P. 680-689.
DOI: 10.1134/S0015462818050142
- Цыпкин Г.Г. Влияние градиента давления и капиллярных сил на образование льда в грунтах // Докл. РАН. 2019. Т. 487. № 2. С. 147-150.
DOI: 10.31857/S0869-56524872147-150
[elibrary]
= Tsypkin G.G. Effect of a pressure gradient and capillary forces on the formation of ice in soils. Doklady Physics. 2019. V. 64. No. 7. P. 304-307.
DOI: 10.31857/10.1134/S1028335819070061
- Alimov M.M., Bazilevsky A.V., Kornev K.G. Minimal surfaces on mirror-symmetric frames: a fluid dynamics analogy // Journal of Fluid Mechanics. 2020. V. 897. A36. P. 1-27.
DOI: 10.1017/jfm.2020.391
- Bazilevsky A.V., Kalinichenko V.A., Plyashkevich V.A., Badazhkov D.V., Rozhkov A.N. Sedimentation of particles in shear flows of viscoelastic fluids with fibers // Rheologica Acta. 2017. V. 56. № 10. P. 787-799.
DOI: 10.1007/s00397-017-1036-x
- Bazilevsky A.V., Rozhkov A.N. Letter: Dome-shaped splashes generated by the impact of a small disk on a sessile water drop // Physics of Fluids. 2018. № 30. P. 101702-1–101702-4.
DOI: 10.1063/1.5055232
- Bulatov V.V., Vladimirov Yu.V. Unsteady regimes of internal gravity wave generation in the ocean // Russian Journal of Earth Sciences. 2018. V. 18. P. ES2004.
DOI: 10.2205/2018ES000619
- Egorov A.V., Nigmatulin R.I., Rozhkov A.N. Temperature effects in deep-water gas hydrate foam // Heat and Mass Transfer. 2019. V. 55. № 2. P. 235-246.
DOI: 10.1007/s00231-018-2403-6
- Gorbunov A., Emelyanov V., Lednev A., Soboleva E. Dynamic and Thermal Effects in Supercritical Fluids under Various Gravity Conditions // Microgravity Science and Technology. 2018. V. 30. № 1-2. P. 53-62.
DOI: 10.1007/s12217-017-9574-5
- Gorbunov A., Soboleva E. Three equations of state of near-critical fluids and numerical simulation of the piston effect // Microgravity Science and Technology. 2020. V. 32. P. 47-57.
DOI: 10.1007/s12217-019-09735-5
- Soboleva E.B. Density-driven convection in an inhomogeneous geothermal reservoir // International Journal of Heat and Mass Transfer. 2018. V. 127 (part C). P. 784-798.
DOI: 10.1016/j.ijheatmasstransfer.2018.08.019
- Tsypkin G.G., Shargatov V.A. Influence of capillary pressure gradient on connectivity of flow through a porous medium // Int. J. Heat and Mass Transfer. 2018. V. 127 (part C). P. 1053-1063.
DOI: 10.1016/j.ijheatmasstransfer.2018.08.107
Экспериментальное оборудование
- Фото-видео аппаратура для регистрации с высоким временным и пространственным разрешением миллисекундных гидродинамических процессов, протекающих в жидких объектах размером от десятков сантиметров до нескольких микрометров; системы непрерывного, импульсного и стробоскопического освещения; цифровой измерительный микроскоп ИМЦ-100; специальные оптические микроскопы, оборудованные видеовыходом и др.
- Лабораторное оборудование, необходимое для приготовления исследуемых жидкостей, – высокоточные электронные весы, системы термостатирования, мешалки и др. Оборудование для реологической характеризации исследуемых жидкостей – ротационные вискозиметры Reotest-2 и HAAKE RotoVisco1, высокочувствительный реометр на воздушных подшипниках HAAKE RS-1. Цифровые системы сбора и анализа данных, поступающих с различных датчиков (давления, перемещения, микрофона и др.).
- Собственные разработки включают Стенд Динамики и структуры осциллирующих течений (ДСО), предназначенный для изучения формирования и разрушения волн Фарадея в жидкости и входящий в список уникального оборудования ИПМех РАН. В число собственных разработок также входят микрореометр «РеоТестБЕР», являющийся прототипом успешного зарубежного коммерческого продукта компании Thermo Haake «CaBER-1»; стенд для изучения формирования и разрушения микрокапель струйного принтера, созданный совместно с компанией Hewlett Packard в ходе работ в рамках соответствующего Научного соглашения между Hewlett Packard Laboratories и ИПМех РАН; 2 стенда для осесимметричного высокоскоростного метания макрообъёмов жидкостей и радиального метания мезообъёмов жидкостей, 2 стенда для моделирования процессов разрушения суспензий твёрдых частиц при сдвиговом течении в плоском и кольцевых каналах, созданных в рамах Научного контракта между Schlumberger Technology Corporation и ИПМех РАН; и другие установки.

Стенд для изучения седиментации частиц в сдвиговых течениях сложных жидкостей
Стенд для изучения седиментации частиц в плоском канале, заполненном суспензией полимерных волокон
Стенд для исследования высокоскоростного радиального метания жидкостей
Информация на август 2020 г.
|
