Федеральное государственное бюджетное учреждение науки Институт проблем механики им. А.Ю. Ишлинского Российской академии наук (ИПМех РАН) Русский Русский
English English

Проезд
Карта сайта
НовостиОб институтеЛабораторииСоветыДиссертационный советОбразованиеКонференции, семинарыЖурналы, книги, ресурсыБиблиотекаПрофсоюзСотрудникам
Главная > Структура > Лаборатории > Механики природных катастроф > детали

Лаборатория механики природных катастроф. Подробная информация

См. также Общие сведения о лаборатории

Общая информация

До 2006  года лаборатория называлась Лабораторией математических методов механики. В 1970–1987 гг. лабораторией заведовала академик П.Я. Кочина, в 1987–2007 годах заведующим лабораторией был академик В.П. Маслов. В разное время в лаборатории работали В.А. Боровиков, М.И. Вишик, В.Б. Лидский, О.В. Голубева, В.В. Козлов, О.А. Олейник, С.Я. Секерж-Зенькович – ученые, внесшие большой вклад в развитие математических методов в механике и физике.

С 2007 г. лабораторией заведует С.Ю. Доброхотов.

Направления исследований

В лаборатории ведутся фундаментальные исследования, охватывающие широкий круг проблем математической и теоретической физики, гидромеханики, геофизической гидродинамики и приложений, термодинамики, теории вероятности, физики наноструктур.

Основные достижения

1. Одно из главных научных направлений исследований лаборатории – развитие асимптотических подходов для конструктивного расчета волновых полей и вихрей в неоднородных средах с учетом эффектов фокусировки и их приложения к задачам механики сплошных сред и квантовой механики. С математической точки зрения можно сказать, что такие подходы – это асимптотические геометрические методы нахождения быстроменяющихся и сингулярных решений линейных и нелинейных уравнений математической физики, включая уравнения гидродинамики, теории упругостей, квантовой механики, оптики, физики плазмы и т.д.

Среди полученных в последнее время сотрудниками лаборатории результатов можно указать развитие методов построения эффективных асимптотических формул для описания решений, порожденных источниками, локализованными в пространстве и времени, и описывающих в том числе, волновые поля в окрестности стандартных и «нестандартных» каустик. К числу последних относятся (3.1.1) фронты волновых полей, описываемых линейными гиперболическими системами, (3.1.2) головные фронты уравнений, включающих дисперсионные эффекты, (3.1.3) береговые линии в задачах о волнах на воде и т.д; с точки зрения дифференциальных уравнений наличие береговой линии в задаче означает вырождение коэффициентов соответствующего уравнения.

Для решения задач такого типа предложены модификации канонического оператора Маслова, основанные на квантовании Фока канонических преобразований и процедуре «униформизации». Найденные асимптотические формулы достаточно легко реализуются в графическом виде с помощью программ Mathematica и Matlab и служат основой быстрых аналитико-численных алгоритмов расчета волновых полей в различных физических процессах. Методы применены к расчету поверхностных и внутренних волн и вихрей в жидкости и атмосфере, возбуждаемых различными источниками, (как мгновенными, так и распределенными во времени), в частности, (3.1.4) построены аналитико-численные алгоритмы расчета распространения и (нелинейного) набега на берег волн цунами и мезомасштабных вихрей в атмосфере, (3.1.6) в рамках гидро-упругой модели в простой и эффективной форме описано поведение длинных волн (волн цунами) в слое воды, порожденных локализованным источником, находящимся в упругом основании.

2. Для спектральных задач для операторов второго порядка с вырождением на границе области (описывающих, например длинные краевые волны и сейши в бассейнах) получены асимптотические функции, связанные с биллиардами с «полужесткими стенками» и с «нестандартными» торами Лиувилля.

3. Предложен обобщенный адиабатический принцип (алгоритм), позволяющий эффективно и достаточно единообразно описать движения в низкоразмерных задачах квантовой и волновой механики. Этот алгоритм, основанный на теории псевдодифференциальных операторов и каноническом операторе Маслова, позволил (3.3.1) описать для широкого диапазона энергий и частот квантовое и классическое движение электронов в различных наноструктурах. В частности, (3.3.2) получены асимптотические формулы, описывающие волновые поля в графене и (3.3.3) оценен вклад влияния иглы электронного микроскопа на результаты измерений. (3.3.4) Обобщенный адиабатический принцип применен для построения асимптотических решений линейных уравнений с быстроосциллирующими коэффициентами в том случае, когда решения уже в главном члене описываются быстроменяющимися функциями и когда известные методы осреднения не работают. В качестве одного из примеров рассмотрены уравнения волн на воде с быстроменяющимися участками дна.

4. С помощью топологических методов исследован эффект Ааронова–Бома в графене и показано, что включение магнитного поля приводит к рождению пар электронных и дырочных уровней в количестве, равном числу квантов потока магнитного поля.

5. Предложенные в п. 1 подходы позволили получить равномерные асимптотические формулы в виде специальных функций не только для уравнений квантовой механики, гидродинамики, оптики и т.д. но и (3.5.1) новые асимптотические формулы для хорошо известных полиномов Эрмита, перекрывающие известные формулы Ротаха–Планшереля.

6. Развита теория квазиклассических асимптотик для дифференциальных уравнений, заданных на графах и перфорированных пространствах. Эта теория применена для описания спектральных свойств сложных наносистем.

7. Построена теория квазиклассических асимптотик с комплексными фазами для широкого класса квантовомеханических и волновых спектральных задач как в конечномерных, так и бесконечномерных ситуациях. (3.7.1) Установлена связь между такими асимптотиками и различными объектами и понятиями классической гамильтоновой механики. Квазиклассические асимптотики с комплексными фазами применены, в частности, (3.7.2) к ряду задач сверхпроводимости и сверхтекучести, (3.7.3) к задачам о гауссовых пучках (включая ситуации с фокальными точками) в плазме, например о гауссовых пучках в ТОКАМАКе.

8. Предложены подходы к анализу режимов охлаждения разрушенного блока реактора Чернобыльской атомной станции.

9. Важные продвижения были получены в последнее время в области исследования надкритических состояний при моделировании сложных процессов в сплошных средах. На основе микроканонического распределения и связанных с ним асимптотических методов (3.9.1) пересмотрены феноменологические законы термодинамики со строгой математической точки зрения, (3.9.2) решен парадокс Гиббса, (3.9.3) существенно исправлены распределения Бозе-Эйнштейна и Максвелла–Больцмана и проведены точные математические оценки. (3.9.4) В термодинамике введена дополнительная переменная – фрактальная размерность, учитывающая в среднем наличие кластеров – и построено соответствующее четырехмерное лагранжево многообразие в восьмимерном фазовом пространстве, которое дает удивительное совпадение с экспериментальными данными. Показано, что применение к этому лагранжеву многообразию туннельного канонического оператора полностью описывает статистические распределения.

10. В рамках космического эксперимента «Ураган» выполнена идентификация ряда систем океанских поверхностных волн, зарегистрированных на фотоснимках с Международной космической станции.

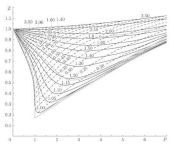
  • Изохоры для метана на плоскости P, Z (давление и фактор сжимаемости)
    Изохоры для метана
    на плоскости P, Z
    (давление и фактор сжимаемости)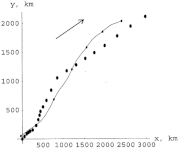
  • Траектория тайфуна реальная (сплошная линия) и рассчитанная по асимптотическим формулам (точки)
    Траектория тайфуна реальная (сплошная линия)
    и рассчитанная по асимптотическим формулам (точки)
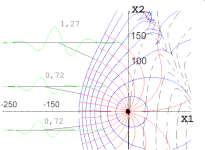
  • Рассчитанные по асимптотическим формулам фронты и волны, возбужденные локализованным источником в бассейне с неровным дном
    Рассчитанные по асимптотическим формулам
    фронты и волны, возбужденные локализованным
    источником в бассейне с неровным дном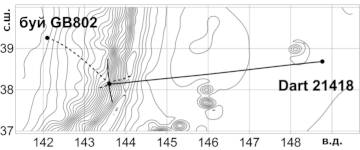
  • Определение местоположения и характеристик источника цунами методом обратных лучей
    Определение местоположения
    и характеристик источника цунами
    методом обратных лучей/li>
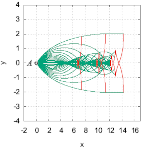
  • Фронты и лучи для волн, распространяющихся над длинным подводным хребтом, рассчитанные с помощью быстрого алгоритма, основанного на вариационном принципе Ферма
    Фронты и лучи для волн,
    распространяющихся над длинным подводным хребтом,
    рассчитанные с помощью быстрого алгоритма,
    основанного на вариационном принципе Ферма
  • Рассчитанные по асимптотическим формулам волны в окрестности клюва каустики на поверхности потенциальной жидкости с нулевой, слабой и сильной дисперсией
    Рассчитанные по асимптотическим формулам
    волны в окрестности клюва
    каустики на поверхности потенциальной жидкости
    с нулевой, слабой и сильной дисперсией
  • На семинаре лаборатории
    На семинаре лаборатории

Образовательная деятельность

Лаборатория тесно связана с Институтом нано-, био-, информационных, когнитивных и социогуманитарных наук и технологий (ИНБИКСТ) Московского физико-технического института. Многие сотрудники лаборатории работают в качестве совместителей на Кафедре математики и математических методов физики МФТИ (зав. кафедрой – С.Ю. Доброхотов), читают лекции и проводят практические занятия в МФТИ по общеобразовательным и специальным математическим дисциплинам. Основная часть аспирантов лаборатории последних лет является выпускниками этой кафедры.

Наиболее значимые публикации сотрудников лаборатории

Книги

  1. Маслов В.П., Федорюк М.В. Квазиклассическое приближение для уравнений квантовой механики. М.: Наука, 1976.
  2. Маслов В.П. Операторные методы. М.: Наука, 1973.
  3. Маслов В.П., Мясников В.П., Данилов В.Г. Математическое моделирование аварийного блока Чернобыльской АЭС. М: Наука, 1987.
  4. Маслов В.П., Шведов О.Ю. Метод комплексного ростка в задаче многих частиц и квантовой теории поля. М: Едиториал УРСС, 2000.
  5. Nazaikinskii V.E., Schulze B.-W., Sternin B. The Localization Problem in Index Theory of Elliptic Operators, Birkhauser, Basel, 2014.
  6. Nazaikinskii V.E., Savin A.Yu., Sternin B.Yu. Elliptic Theory and Noncommutative Geometry. Birkhauser, Basel, 2008.

Статьи

  1. Доброхотов С.Ю., Назайкинский В.Е. Асимптотики волновых и вихревых локализованных решений линеаризованных уравнений мелкой воды, в сборнике «Актуальные проблемы Механики», посвященный 50-летию Института проблем механики им. А.Ю. Ишлинского РАН, М., Наука, 2015, с. 98-139.
  2. Belov V.V. , Dobrokhotov S.Yu., Tudorovskiy T.Ya. Operator Separation of Variables for Adiabatic Problems in Quantum and Wave Mechanics, J. Engng. Math., 2006, 55 (1-4), p. 183-237. DOI: 10.1007/s10665-006-9044-3
  3. Dobrokhotov S.Yu., Shafarevich A.I., Tirozzi B. Localized wave and vortical solutions to linear hyperbolic systems and their application to linear shallow water equations, Russ. J. Math. Phys., 2008. Vol. 15, No. 2, p. 192-221. DOI: 10.1134/S1061920808020052
  4. Reijnders K.J.A., Minenkov D.S., Katsnelson M.I., Dobrokhotov S.Yu. Electronic optics in graphene in the semiclassical approximation, Annals of Physics, 2018, 397, p. 65-135. DOI: 10.1016/j.aop.2018.08.004
  5. Katsnelson M.I., Nazaikinskii V.E. Partial spectral flow and the Aharonov–Bohm effect in graphene, Eur. Phys. J. C, 2020, Article no. 80:888. DOI: 10.1140/epjc/s10052-020-08464-z
  6. Доброхотов С.Ю., Назайкинский В.Е., Шафаревич А.И. Новые интегральные представления канонического оператора Маслова в особых картах, Изв. РАН. Сер. Матем., 2017, 81:2, с. 53-96. DOI: 10.4213/im8470
    = Dobrokhotov S.Yu., Nazaikinskii V.E., Shafarevich A.I. New integral representations of the Maslov canonical operator in singular charts, Izvestiya: Mathematics. 2017, V.&nbap;81, No. 2, p. 286-328. DOI: 10.1070/IM8470
  7. Dobrokhotov S.Yu., Grushin V.V., Sergeev S.A., Tirozzi B. Asymptotic theory of linear water waves in a domain with nonuniform bottom with rapidly oscillating sections, Russian Journal of Mathematical Physics, 2016, Vol. 23, no. 4., p. 455-474. DOI: 10.1134/S1061920816040038
  8. Караева Д.А., Караев А.Д., Назайкинский В.Е. Метод осреднения в задаче о распространении длинных волн от локализованного источника в бассейне над неровным дном, Дифференц. Уравнения, 2018, 54:8, с. 1075-1089. DOI: 10.1134/S037406411808006X
    = Karaeva D.A., Karaev A.D., Nazaikinskii V.E. Homogenization Method in the Problem of Long Wave Propagation from a Localized Source in a Basin over an Uneven Bottom, Differential Equations, 2018, V. 54, No. 8, p. 1057-1072. DOI: 10.1134/S0012266118080062
  9. Аникин А.Ю., Доброхотов С.Ю., Назайкинский В.Е., Цветкова А.В. Асимптотики собственных функций оператора ∇D(x)∇ в двумерной области, вырождающегося на её границе, и биллиарды с полужёсткими стенками, Дифференциальные уравнения, 2019, т. 55, № 5, с. 660-672. DOI: 10.1134/S0374064119050078
    = Anikin A.Yu., Dobrokhotov S.Yu., Nazaikinskii V.E., Tsvetkova A.V. Asymptotic Eigenfunctions of the Operator ∇D(x)∇ Defined in a Two-Dimensional Domain and Degenerating on Its Boundary and Billiards with Semi-Rigid Walls, Differential Equations, 2019, V. 55, No. 5, p. 644-657 DOI: 10.1134/S0012266119050069
  10. Аникин А.Ю., Доброхотов С.Ю., Клевин А.И., Тироцци Б. Гауссовы пакеты и пучки с фокальными точками в векторных задачах физики плазмы, Теор. и мат.физика, 2018, 196:1, с. 135-160. DOI: 10.4213/tmf9520
    = Anikin A.Yu., Dobrokhotov S.Yu., Klevin A.I., Tirozzi B. Gaussian Packets and Beams with Focal Points in Vector Problems of Plasma Physics, Theoretical and Mathematical Physics, 2018, V. 196, No. 1, p. 1059-1081. DOI: 10.1134/S0040577918070115
  11. Аникин А.Ю., Доброхотов С.Ю., Назайкинский В.Е., Руло М. Канонический оператор маслова на паре лагранжевых многообразий и асимптотика решений стационарных уравнений с локализованными правыми частями, Доклады Академии Наук, 2017, т. 475, № 6, с. 624-628. DOI: 10.7868/S0869565217240057
    = Anikin A.Yu., Dobrokhotov S.Yu., Nazaikinskii V.E., Rouleux M. The Maslov canonical operator on a pair of Lagrangian manifolds and asymptotic solutions of stationary equations with localized right-hand sides, Doklady Mathematics, 2017, V. 96, No. 1, p. 406-410. DOI: 10.1134/S1064562417040275
  12. Dobrokhotov S.Yu., Petrov P.N. Asymptotics of Linear Surface Waves Generated by a Localized Source Moving Along the Bottom of the Basin. I. One-Dimensional Case, Russian Journal of Mathematical Physics, 2019, V. 26, No. 1, p. 32-39. DOI: 10.1134/S1061920819010035
  13. Dobrokhotov S.Yu., Nazaikinskii V.E., Tolchennikov A.A. Uniform Formulas for the Asymptotic Solution of a Linear Pseudodifferential Equation Describing Water Waves Generated by a Localized Source, Russian Journal of Mathematical Physics, 2020, V. 27, No. 2, p. 185-191. DOI: 10.1134/S1061920820020041
  14. Доброхотов С.Ю., Назайкинский В.Е. Эффективные асимптотики в задачах о распространении волн, порожденных локализованными источниками, в линейных многомерных неоднородных и дисперсных средаx, Журнал вычислительной математики и математической физики, 2020, т. 60, № 8, с. 1394-1407. DOI: 10.31857/S0044466920080062
    = Dobrokhotov S.Yu., Nazaikinskii V.E. Efficient Asymptotics in Problems on the Propagation of Waves Generated by Localized Sources in Linear Multidimensional Inhomogeneous and Dispersive Media, Computational Mathematics and Mathematical Physics, 2020, V. 60, p. 1348-1360
  15. Маслов В.П. Новые формулы, связанные с аналитической теорией чисел, и их приложение к статистической физике, ТМФ, 2018, 196:1, с. 161-166. DOI: 10.4213/tmf9597
    =  Maslov V.P. New Formulas Related to Analytic Number Theory and Their Applications in Statistical Physics, Theoretical and Mathematical Physics, 2018, V. 196, No. 1, p. 1082-1087. DOI: 10.1134/S0040577918070127
  16. Allilueva A.I., Shafarevich A.I. Asymptotic solutions for MHD systems with a rapid jump near a moving surface, Fluid Dynamics Research. 2018, Vol. 50, No. 1. DOI: 10.1088/1873-7005/aa769a
  17. Доброхотов С.Ю., Ильясов Х.Х., Толстова О.В. Простые решения линейной задачи о возбуждении длинных волн на поверхности жидкости источником в упругом основании, Известия Российской Академии Наук. Механика твердого тела, 2020, № 4, с. 126-139. DOI: 10.31857/S0572329920040030
    = Dobrokhotov S.Yu., Ilyasov Kh.Kh., Tolstova O.L. Simple Solutions to the Linear Problem of the Generation of Long Waves on the Surface of a Liquid by a Source in an Elastic Foundation Bottom, Mech. Solids., 2020, V. 55, No. 4, p. 561-572 DOI: 10.3103/S0025654420040032
  18. Цветкова А.В., Шафаревич А.И. Локализованное асимптотическое решение волнового уравнения с переменной скоростью на простейшем декорированном графе, Труды Математического института им. В.А. Стеклова РАН, 2020, Т. 308, с. 265-275. DOI: 10.4213/tm4069
    = Tsvetkova A.V., Shafarevich A.I. Localized Asymptotic Solution of a Variable-Velocity Wave Equation on the Simplest Decorated Graph, Proceedings of the Steklov Institute of Mathematics, 2020, V. 308, p. 250-260 DOI: 10.1134/S0081543820010204
  19. Доброхотов С.Ю., Макракис Г., Назайкинский В.Е. Канонический оператор Маслова, одна формула Хёрмандера и локализация решения Берри–Балажа в теории волновых пучков, ТМФ, 2014, 180:2, с. 162-188. DOI: 10.4213/tmf8683
    = Dobrokhotov S.Yu., Makrakis G.N., Nazaikinskii V.E. Maslov's canonical operator, Hormander's formula, and localization of the Berry-Balazs solution in the theory of wave beams, Theoretical and Mathematical Physics, 2014, V. 180, No. 1, p. 894-916 DOI: 10.1007/s11232-014-0187-5
  20. Nazaikinskii V.E., Bedrikovetsky P.G., Kuzmina L.I., Osipov Y.V. Exact solution for deep bed filtration with finite blocking time, SIAM J. Appl. Math., 2020, 80:5, p. 2120-2143. DOI: 10.1137/19M1309195

Информация на октябрь 2020 г.