Laboratory of Complex Fluid Mechanics. Details
See also Laboratory general information
Main achievements
- The effect of suppressiоn of breakup process and regularization of a standing gravitational wave using a layer of floating particles has been established (Kalinichenko V.A., 2019).
- Pulse radial outflow of fluid from the gap between two rapidly approaching discs is used as a method for rheological testing of elastic fluids in the regime of extreme deformations (high strain rates and tensile degrees). A theoretical description of the radial outflow of an elastic fluid is constructed within the framework of the Oldroyd-B rheological model. Test experiments on the throwing of aqueous solutions of high molecular weight polyethylene oxide (PEO) with concentrations 1, 2, 4%. By comparing theoretical predictions with experimental data, the rheological characteristics of the tested PEO solutions were determined under extreme deformation conditions. There is a significant increase in the modulus of elasticity and a decrease in the relaxation time at high strain rates. The method is applicable for rheological testing of polymer and biological fluids in medicine, biology, and in a number of chemical technologies (Bazilevsky A.V., Rozhkov A.N., 2018).

The liquid is radially ejected at a speed of ~1-10 m/s from the annular gap between two approaching disks; the initial thickness of the gap is ~2 mm, the outflow time is ~1 ms: (a-e) – water, glycerin, polyethylene oxide solutions of concentrations of 0.1, 1, 2 and 4%. The position of the gap is indicated by an arrow.
- A numerical simulation of the gravitational concentration convection of water with a dissolved impurity in a rectangular geothermal reservoir, at the upper boundary of which a constant impurity concentration is maintained, has been performed. It was found that small-scale salt "fingers" appear chaotically near the upper boundary, which merge and enlarge when descending; over time, the emerging small-scale "fingers" are combined into groups. The influence of porosity on the time of convection development and characteristics of mass transfer in a homogeneous geothermal system is investigated (Soboleva E.B. and Tsypkin G.G., 2016).
- The deformation of the water-saturated area during filtration in a porous medium with varying capillary pressure was investigated. It is shown that in the case of flow instability, the capillary pressure gradient directed along the interface between the liquid and gas leads to deformation of the region, which eventually divides into two unconnected regions. It is assumed that the process under consideration describes one of the possible mechanisms of fragmentation of filtration currents, which can lead to the formation of residual oil during the operation of oil fields and salinization of soils during the evaporation of groundwater containing a dissolved impurity (Tsypkin G.G. and Shargatov V.A., 2018).
- A numerical simulation of the temperature growth of the supercritical fluid due to the piston effect (heating during adiabatic compression, which occurs due to the high compressibility of the medium) has been performed. It was found that near the critical point at the characteristic time of the piston effect it ceases to decrease and tends to a constant value, deviating from the theoretically predicted dependence, which indicates the nonlinear nature of the phenomenon. At sufficiently large temperatures, the heating goes into thermal conductivity mode. Here ε=(T–Tc)/Tc is the temperature "distance" to the critical point; T, Tc are current and critical temperature values (Gorbunov A. and Soboleva E., 2020).
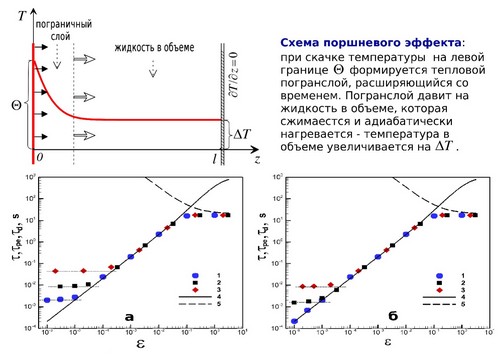
The time of the piston effect τ with a temperature jump Θ=0.1 (1), 1 (2), 10 mK (3) in a region 1 cm wide, as function of ε. The media is described by the cubic van der Waals equation (a) or the fifth degree equation of state (b). Theoretical curve of the piston effect τpe(ε) (4), thermal conductivity curve τd(ε) (5).
- The results of mathematical modeling of unsteady modes of generation of internal and surface gravitational ones show that wave fields from unsteady sources of disturbances under certain modes of generation are a hybrid system of waves of two types: annular (transverse) and wedge-shaped (longitudinal). The nonstationarity of the source of disturbances leads to the appearance not only of ring waves diverging directly from the source, but also to the generation of hybrid wave disturbances propagating from the source upstream. The qualitative picture of wave fields from a non-stationary source is significantly complicated in comparison with the case of wave generation by a moving stationary source, when wave fronts of separate wedge-shaped (longitudinal) modes successively arrive at a fixed observation point. With certain generation parameters, circular (transverse) waves can initially arrive at a fixed observation point. The wave modes that first reach a fixed observation point are determined by the generation parameters and stratification of the medium. For large mode numbers, the half-angle of the Kelvin wave wedge decreases with the mode number in the same way as for the cases of stationary lasing regimes. The obtained results of mathematical modeling of the fields of internal and surface gravitational waves make it possible to effectively analyze the main amplitude-phase characteristics of the excited wave fields, and, in addition, qualitatively investigate the solutions obtained, which is important for the correct formulation of more complex mathematical models of wave dynamics of real stratified media. Such wave patterns can be observed during remote sensing, observation and measurements of internal and surface gravitational waves excited by various sources of disturbances in natural (ocean, Earth's atmosphere) and artificial stratified media (Bulatov V.V. and Vladimirov Y.V., 2018).
History
The basis for the creation of the Laboratory of the Mechanics of Complex Fluids was the Laboratory of Applied Continuum Mechanics, which until 1994 was headed by Professor Vladimir Markovich Entov, and the Laboratory of Mathematical and Physical Modeling in Hydrodynamics, headed until 2010 by Professor Vadim Ivanovich Polezhaev. At present, the laboratory is headed by Doctor of Sciences Aleksey Nikolaevich Rozhkov.
General information
The Laboratory of the Mechanics of Complex Fluids continues and develops the research initiated in the laboratories of the Institute for Problems of Mechanics, which at different times were led by professors Lev Alekseevich Chudov, Vadim Bronislavovich Librovich, Vladimir Markovich Entov and Vadim Ivanovich Polezhaev.
Today the laboratory consists of 7 doctors и 5 candidates of sciences. At various times, the laboratory staff has got scientific awards: the RAS Prize named after K.E. Tsiolkovsky (V.I. Polezhaev, S.A. Nikitin, 2003); Prize named after G.I. Petrov (V.I. Polezhaev, O.A. Bessonov, A.A. Gorbunov, S.A. Nikitin, E.B. Soboleva, 2006); Prizes named after G.V. Vinogradov of Rheological Society (A.V. Bazilevsky and A.N. Rozhkov, 2017); Prize and medal after L.I. Sedova (G.G. Tsypkin, 2017); Tanasawa Award, Institute of Liquid Atomization and Spray Systems – International (A. Rozhkov, 2009).
Main publications
Books
- Bulatov V.V., Vladimirov Yu.V. A general approach to ocean wave dynamics research: modelling, asymptotics, measurements. М.: Издательство «ОнтоПринт», 2019. 587 с. ISBN 978-5-00121-132-7
- Цыпкин Г.Г. Течения с фазовыми переходами в пористых средах. М.: Наука. Физматлит. 2009. 230 с.
ISBN 978-5-9221-1102-7
Papers
- Alimov M.M., Bazilevsky A.V., Kornev K.G. Minimal surfaces on mirror-symmetric frames: a fluid dynamics analogy. Journal of Fluid Mechanics. 2020. V. 897. A36. P. 1-27.
DOI: 10.1017/jfm.2020.391
- Bazilevsky A.V., Kalinichenko V.A., Plyashkevich V.A., Badazhkov D.V., Rozhkov A.N. Sedimentation of particles in shear flows of viscoelastic fluids with fibers. Rheologica Acta. 2017. V. 56. No. 10. P. 787-799.
DOI: 10.1007/s00397-017-1036-x
- Bazilevsky A.V., Rozhkov A.N. Letter: Dome-shaped splashes generated by the impact of a small disk on a sessile water drop. Physics of Fluids. 2018. No. 30. P. 101702-1–101702-4.
DOI: 10.1063/1.5055232
- Bazilevskii A.V., Kalinichenko V.A., Rozhkov A.N. Viscous Regularization of Breaking Faraday Waves. JETP Letters. 2018. V. 107. No. 11. P. 684-689.
DOI: 10.1134/S0021364018110061
- Bazilevskii A.V., Rozhkov A.N. Splash of an elastic liquid as a rheological test of polymer solutions. Polymer Science. Series A. 2018. V. 60. No. 3. P. 391-403.
DOI: 10.1134/S0965545X1803001X
- Bulatov V.V., Vladimirov Y.V. Analytical solutions of the internal gravity wave equation for a semi-infinite stratified layer of variable buoyancy. Computational Mathematics and Mathematical Physics. 2019. V. 59. No. 5. P. 747-750.
DOI: 10.1134/S0965542519050051
- Bulatov V.V., Vladimirov Y.V. Far fields of internal gravity waves from a nonstationary source. Oceanology. 2018. V. 58. No. 6. P. 796-801.
DOI: 10.1134/S0001437018060036
- Bulatov V.V., Vladimirov Y.V. Internal waves excited by a moving source in a medium of variable buoyancy. Fluid Dynamics. 2018. V. 53. No. 5. P. 616-622.
DOI: 10.1134/S001546281805004X
- Bulatov V.V., Vladimirov Yu.V. Unsteady regimes of internal gravity wave generation in the ocean. Russian Journal of Earth Sciences. 2018. V. 18. P. ES2004.
DOI: 10.2205/2018ES000619
- Fedyushkin A.I. Effect of convection on crystal growth of calcium phosphate in a thermostat under terrestrial and space conditions. Fluid Dynamics. 2020. V. 55. No. 4. P. 465-476.
DOI: 10.1134/S0015462820040047
- Gorbunov A., Soboleva E. Three equations of state of near-critical fluids and numerical simulation of the piston effect. Microgravity Science and Technology. 2020. V. 32. P. 47-57.
DOI: 10.1007/s12217-019-09735-5
- Gorbunov A., Emelyanov V., Lednev A., Soboleva E. Dynamic and Thermal Effects in Supercritical Fluids under Various Gravity Conditions. Microgravity Science and Technology. 2018. V. 30. No. 1-2. P. 53-62.
DOI: 10.1007/s12217-017-9574-5
- Egorov A.V., Nigmatulin R.I., Rozhkov A.N. Temperature effects in deep-water gas hydrate foam. Heat and Mass Transfer. 2019. V. 55. No. 2. P. 235-246.
DOI: 10.1007/s00231-018-2403-6
- Kalinichenko V.A. Regularization of barotropic gravity waves in a two-layer fluid. Fluid Dynamics. 2019. V. 54. No. 6. P. 761-773.
DOI: 10.1134/S0015462819060065
- Soboleva E.B. Adiabatic heating (cooling) of a supercritical fluid with variation in its physical properties. Fluid Dynamics. 2017. V. 52. No. 1. P. 25-36.
DOI: 10.1134/S0015462817010033
- Soboleva E.B., Tsypkin G.G. Regimes of haline convection during the evaporation of groundwater containing a dissolved admixture. Fluid Dynamics. 2016. V. 51. No. 3. P. 364-371.
DOI: 10.1134/S001546281603008X
- Soboleva E.B. Density-driven convection in an inhomogeneous geothermal reservoir // International Journal of Heat and Mass Transfer. 2018. V. 127 (part C). P. 784-798.
DOI: 10.1016/j.ijheatmasstransfer.2018.08.019
- Tsypkin G.G., Shargatov V.A. Influence of capillary pressure gradient on connectivity of flow through a porous medium // Int. J. Heat and Mass Transfer. 2018. V. 127 (part C). P. 1053-1063.
DOI: 10.1016/j.ijheatmasstransfer.2018.08.107
- Tsypkin G.G. Thermodynamic conditions of formation of CO2 hydrate in carbon dioxide injection into a methane hydrate reservoir. Fluid Dynamics. 2018. V. 53. No. 5. P. 680-689.
DOI: 10.1134/S0015462818050142
- Tsypkin G.G. Effect of a pressure gradient and capillary forces on the formation of ice in soils. Doklady Physics. 2019. V. 64. No. 7. P. 304-307.
DOI: 10.31857/10.1134/S1028335819070061
Experimental equipment
- Photo and video equipment for recording with high temporal and spatial resolution of millisecond hydrodynamic processes occurring in liquid objects ranging in size from tens of centimeters to several micrometers; continuous, pulsed and stroboscopic lighting systems; digital measuring microscope; special optical microscopes equipped with a video output, etc.
- Laboratory equipment required for the preparation of the studied liquids: high-precision electronic scales, thermostating systems, stirrers, etc. Equipment for rheological characterization of the studied liquids - rotational viscometers Reotest-2 and HAAKE RotoVisco1, high-sensitivity rheometer on air bearings HAAKE RS-1. Digital systems for collecting and analyzing data from various sensors (pressure, displacement, microphone, etc.).
- Own developments include the Setup of Oscillating Flow Dynamics and Structure, designed to study the formation and breakup of Faraday waves in a liquid and included in the List of unique equipment of IPMech RAS. Our own developments also include the RheoTestBER micro-rheometer, which is a prototype of the successful foreign commercial product "CaBER-1" of Thermo Haake company; a setup for studying the formation and breakup of inkjet printer microdroplets, created together with Hewlett Packard in the framework of the Scientific Agreement between Hewlett Packard Laboratories and IPMech RAS; 2 setups for axisymmetric high-speed throwing of macrovolumes of liquids and radial throwing of mesovolumes of liquids, 2 setups for modeling the processes of destruction of suspensions of solid particles during shear flow in flat and annular channels, created in the framework of the Scientific contract between Schlumberger Technology Corporation and IPMech RAS; and other settings.

Setup for studying the sedimentation of particles in shear flows of complex fluids
Setup for studying the sedimentation of particles in a flat channel filled with a suspension of polymer fibers
Setup for research of high-speed radial throwing of liquids
|
